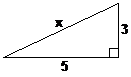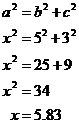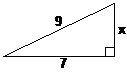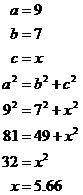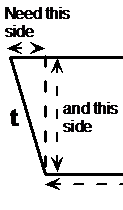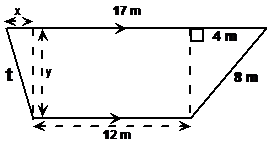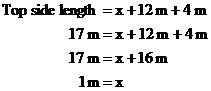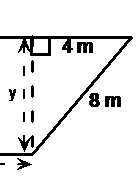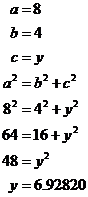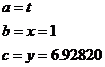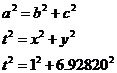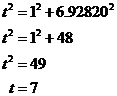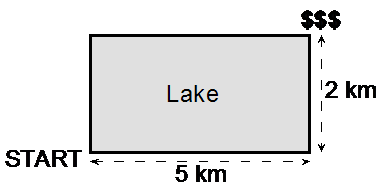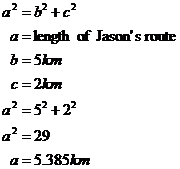Say a question describes a triangle as ‘triangle ABC’, with a right angle at B. How do you draw a diagram of this triangle?
First of all, you should realise that you’ve only been given a little bit of information in the question, so different people will probably draw different triangles. But they must have a few things in common:
Sponsored Links
· The triangles must have 3 sides and 3 corners. The corners are what the ‘ABC’ letters represent – one corner is labelled ‘A’, one is labelled ‘B’ and one is labelled ‘C’.
· You need to have a right angle in the ‘B’ corner.
So that’s all the restrictions there are on what triangle you draw. This means that you could draw any of these triangles and it would be fine:
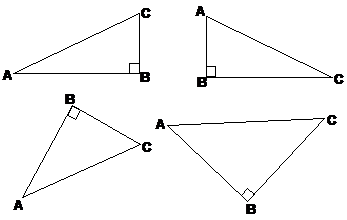
Usually it’s easiest to draw one which is sort of in a ‘normal’ orientation, like one of the top two, which have one horizontal and one vertical side.
Specifying the hypotenuse side
Sometimes you’ll be asked to work out which side in a right-angled triangle is the hypotenuse. It is always the side opposite the right angle. So for the triangles in the previous diagram, side AC is the hypotenuse because it is the side opposite the 90° angle in corner B.
Checking whether a triangle is right-angled
Sometimes you’ll get given a triangle and be asked to use Pythagoras’ Theorem to check whether the triangle is a right-angled triangle. How do you do this? Well, you take the side lengths and put them into the equation, and if the equation works, this means it is a right-angled triangle. Often the question will have the triangle drawn as if it is a right-angled triangle even when it isn’t, just to try and trick you. Don’t be fooled! Take this triangle for instance:
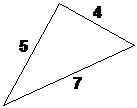
How do we test this triangle using Pythagoras’ Theorem? Well, the theorem is that:
![]()
Remember that ‘a’ is always the longest side in the triangle, and ‘b’ and ‘c’ are the two other sides. So what we can do is calculate what each side of this equation equals for our triangle, and then see if the two sides of the equation equal each other. If they do, then it is a right-angled triangle.
First, the left hand side:
![]()
The longest side in our triangle is ‘7’. So this becomes:
![]()
Now we can do the right hand side of the equation:
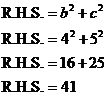
Now, if the triangle is right-angled, the equation’s left hand side has to equal the right hand side. However, for our triangle, our L.H.S. works out to 49, but our R.H.S. is only 41, so they’re not equal. This means our triangle is not a right-angled triangle. In your solution you’d probably want to write something like this:
If a = 7, b = 4 and c = 5 then ![]() for this triangle, which
means that the triangle is not a right-angled triangle.
for this triangle, which
means that the triangle is not a right-angled triangle.
Proving Pythagoras’ Theorem
There are lots and lots of ways of proving that Pythagoras’ Theorem is correct for any right-angled triangle. Most of them involve playing with triangles and re-arranging them around to form more complicated shapes. Here’s one of the simpler proofs. It’s good to understand how a theorem is proven – understanding how something works is always much better than just memorising the theorem. Especially in an exam under pressure – if you understand it you’re less likely to forget it than if you have just memorised some formula.
So on to the proof, what we need to do is start with 4 identical right-angled triangles. It doesn’t matter what shape they are as long as they are right-angled, and as long as each of the 4 are identical to each other.
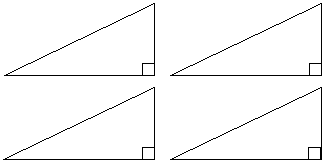
Easy so far right? Now, this is the tricky bit. When mathematicians prove anything in mathematics, it generally involves playing around with a whole lot of things before they finally work out a good proof. It’s rare that they get it first go. So for this proof, people had to play around with arranging these triangles in lots of different layouts trying to find a layout which would help them prove the theorem. Finally, they came up with this arrangement:
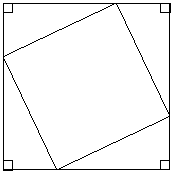
The four triangles are arranged to form a sort of boundary around a central space. The central space is a square. We can label the side lengths in the diagram with letters, using ‘a’ to represent the hypotenuse of the triangles, and ‘b’ and ‘c’ to represent the other sides:
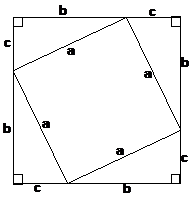
To prove theorems in mathematics, you often have to use some stuff you already know to help you prove it. For instance, in this case, the diagram has triangles and squares in it. We already know how to work out the areas of these triangles and squares. We can use our knowledge of areas to help us prove Pythagoras’ Theorem.
Now, there are actually two squares in this diagram. There’s the square between all the triangles, but there’s also the larger square formed by the outer boundary of all the shapes:
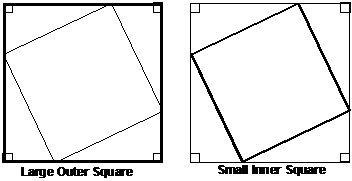
We can write a relationship involving the area of the larger square, the area of the smaller square, and the areas of the 4 triangles. What do you think the area of the triangles is equal to? Well, it’s equal to the area of the large square minus the area of the smaller square. You could even write an equation using the shapes like this:

We can work out what each of these areas is and write a proper equation with letters instead of shapes.
![]() Area
of the four triangles
Area
of the four triangles
OK, what’s the area of the four triangles? Well, how about one triangle first? We know that the area of a triangle is one half times the base times the height:
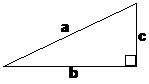
![]()
For our triangle, let’s use ‘b’ as the base, and ‘c’ as the height:
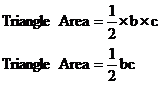
But we’ve got four triangles, so their total area is:
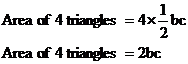
![]() Area
of large square
Area
of large square
The area of the large square is easy to find, it’s just the side length squared. What is its side length? Well, a side of the big square looks like this:
![]()
So its length is ‘b + c’.
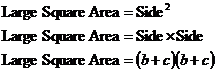
![]() Area
of small square
Area
of small square
It’s a square, so it’s also easy to find out the area for. What is its side length? The side length is just ‘a’, shown in the diagram:
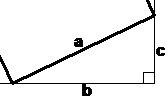
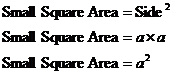
Putting it all together
So now we’ve got the three areas, we can put them into our equation:
![]()
![]()
Now when you’re trying to prove something, you’ve
got to always keep in mind what you’re trying to get to in the end. In our
case, we’re trying to get to ![]() . We’ve already got an equation
with ‘a’s, ‘b’s and ‘c’s in it. We’ve just got to try and rearrange it so
that it ends up looking like
. We’ve already got an equation
with ‘a’s, ‘b’s and ‘c’s in it. We’ve just got to try and rearrange it so
that it ends up looking like ![]() . So let’s start:
. So let’s start:
![]()
First let’s multiply out those brackets:
![]()
Now we’ve got a ‘2bc’ term on both sides – these will cancel out, leaving us with:
![]()
One more step to get it into the final form, let’s add ‘a2’ to both sides:
![]()
Yeeha! We’ve got it into the exact same form as Pythagoras’ Theorem. Let’s check that the ‘a’s, ‘b’s and ‘c’s correspond to the right sides. If this is exactly the same as Pythagoras’ Theorem, then the ‘a’ should represent the longest side of the triangles, the hypotenuse. Check the diagrams – it does! And ‘b’ and ‘c’ represent the other sides of the triangles, like in Pythagoras’ Theorem.
So by using some simple knowledge of how areas are calculated, we have managed to show how you get Pythagoras’ Theorem. This is called deriving a proof – working through some calculations to end up with the equation or theorem you’re trying to prove.
Using Pythagoras’ Theorem to work out side lengths
Okay, so a very common question you’ll get is a triangle with only two of its three sides labelled with a length, and you’ll have to work out the length of the third side. Often the unknown third side’s length will be labelled ‘x’ or ‘a’ or something else. So you’ll be asked something like, “Find x.” There are two main situations you’ll encounter:
|
Find x:
|
|
Solution |
|
In this case, all you do is take your theorem,
Some teachers might like you to do something like this before you start calculating as well, just to tell them exactly what you’re doing:
The other type of question gives you a triangle with a known hypotenuse, but an unknown other side: |
|
Find x:
|
|
Solution |
|
In this case, you start with the theorem, but this time you know what ‘a’, the hypotenuse is – it’s ‘9’ in this case. The other side you know can go in as either ‘b’ or ‘c’. If the ‘7’ goes in as ‘b’, then ‘x’ is going to be ‘c’. If the ‘7’ goes in as ‘c’, then the ‘x’ is going to be ‘b’. In this case, let’s put ‘7’ in as ‘b’:
|
Significant figures and diagrams
How many significant figures should you write your answer to? Well, if the question asks for a specific number of significant figures, then just go by the question. For instance, it may ask for two significant figures, in which case your answer for the last question would be:
![]()
However, sometimes the question won’t tell you how many significant figures are required. In this sort of situation, you need to look at how many significant figures are given in the diagram. ‘9’ and ‘7’ are numbers with only one significant figure. This would suggest you give your answer to only one significant figure:
![]()
However, you’d actually have a reasonable chance of guessing an answer to this sort of accuracy. To show the teacher that you’ve actually calculated the answer properly, I usually give two significant figures or the number of significant figures presented in the diagram, whichever is greater. So in this case, although there’s only one significant figure in the diagram numbers, I’d still give two significant figures in my answer:
![]()
Handy Hint #1 - Making an estimate of the side length
It’s often good to make an estimate of what you think the answer will be, which you can compare with the answer you actually calculate. When you’re working with triangles and Pythagoras’ Theorem, you can use estimates to help check your answers.
There are always a few simple things you can check:
- What side length are you trying to find? If you’re trying to find the length of the hypotenuse, then you should get an answer which is larger than either of the other two sides. If you’re trying to find one of the other sides, then you should get an answer which is smaller than the length of the hypotenuse.
- If you’re trying to find the length of the hypotenuse, it will always be smaller than the sum of the other two sides.
- Same goes for the reverse – if you’re trying to find the length of a side which isn’t the hypotenuse, then its length plus the other short side should add up to more than the length of the hypotenuse.
Say we have a right-angled triangle like this one, and we need to find ‘a’:
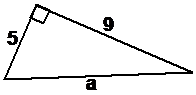
First of all, which side is ‘a’ – is it the hypotenuse? It’s opposite the corner with the 90 degree angle, so this means that it is the hypotenuse, the longest side in the triangle. So first up, we should expect ‘a’ to be larger than either ‘5’ or ‘9’, so larger than ‘9’ in other words.
Secondly, the length of the hypotenuse will always be smaller than the sum of the other two sides. 5 plus 9 is 14, so we expect our hypotenuse length to be smaller than 14.
This means that we should expect our answer for the length of the hypotenuse to be larger than 9, but smaller than 14. If you use the actual theorem, you can work out your answer:
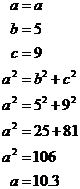
Does this check with what we estimated? Well, 10.3 is definitely larger than 9, and it’s also smaller than 14. This tells us that our answer is a ‘reasonable’ one and gives us some confidence that we’ve got it right.
More complicated Pythagoras’ Theorem questions
Some of the more complicated questions don’t just have triangles in them, but more complicated shapes as well. For instance, you might get triangles within other triangles, or other shapes like squares or rectangles. Here’s an example of a slightly harder question you might get:
|
Find the value of ‘t’ in this diagram:
|
|
Solution |
|
This question is a bit harder to answer because you can’t just plug numbers straight into Pythagoras’ Theorem to get the value of ‘t’. ‘t’ is the hypotenuse of a triangle, but we need to know the lengths of the other two sides before we can use the theorem.
So we need to set about finding the lengths of these other two sides. The shortest one we can find straight away, by comparing the top and bottom horizontal sides of the trapezium. We know the middle part of the top horizontal side has to be the same length as the bottom horizontal side – 12 metres. We can write an equation for the total length of the top horizontal side, which we know is 17 metres long. It will make it easier for us if we label some of the sides so we can refer to them more easily in our equation:
So now we know the length of one of the triangle’s sides, which we have called ‘x’. We need to work out the length of the other side – the vertical side. We have no way of working this out directly, but if you look at the triangle on the right hand side of the diagram, you’ll notice it also has a vertical side the exact same length as the one we’re trying to find out, which we’ve labelled ‘y’. The difference is, in this other triangle, we know the other two sides, so we can use Pythagoras’ Theorem to work out the length of the vertical side:
Using Pythagoras’ Theorem, we can work out what ‘y’ is: Notice how I’ve written the answer for ‘y’ with a few intermediate decimal places. This is because this is not the final answer, but rather an answer we need to use to get the final answer. If you round off too early in the question, your final answer won’t be anywhere near as accurate as it could be. This is a great situation in which to use the memory function on your calculator to store the value of ‘y’ you worked out. And so now we have values for both ‘x’ and ‘y’ – we’ve got two sides of our triangle, so we can now work out what ‘t’ is. We just need to use Pythagoras’ Theorem again. First we need to say what ‘a’, ‘b’ and ‘c’ are going to be in the equation: Here I’ve said that ‘a’, which represents the hypotenuse, is ‘t’, which is the name of the hypotenuse in the diagram. ‘b’ is one of the other sides, I’ve used it to represent x, which I’ve also written a value for. ‘c’ I’ve use to represent the other side – side ‘y’, and I’ve also written the value we calculated for it. Now we can write Pythagoras’ Theorem and put our values into it: Here’s a neat trick to remember. 6.92820 is our value of ‘y’. In the last line of the calculation above, this value is squared. Now how did we get ‘y’ in the first place? If you look back a little bit, you’ll see a line that says: So if we need to square ‘y’, we can just write ‘48’ instead: What have I forgotten? Well, the distances in our diagram were marked in metres. So I should remember to put units in the answer: |
Pythagorean Triples
You may notice that most of the time, when you use Pythagoras’ Theorem to calculate the length of a side, you get an answer which isn’t a whole number – it has decimal places. However, there are a few right-angled triangles where the lengths of all the sides are whole numbers. The sets of three side lengths for these triangles are known as Pythagorean Triples or Pythagorean Triads. The simplest triple is a triangle with side lengths 3, 4 and 5:
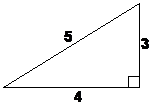
You can check that this works in Pythagoras’ Theorem:
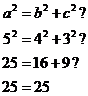
Now, you can scale the size of the triangle and its sides will still form a Pythagorean Triple. For instance, I could make this triangle twice as big:
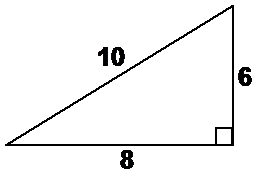
The only way to actually work out all the different triangles that make up the Pythagorean Triples is to use trial and error and go through lots of possible combinations of side lengths. Because triangles of this type often turn up on exams, it’s worth your while to memorise some of the most common triples:
3, 4, 5
5, 12, 13
12, 16, 20
8, 15, 17
If you know these off by heart often in a question you can save yourself any calculating if you recognise that two of the sides form part of a Pythagorean Triple. For instance, check out this triangle:
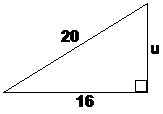
‘16’ and ‘20’ form part of the Pythagorean Triple 12, 16, 20. This means that without having to do any calculation at all, we can work out that ‘u’ is going to equal 12. Be careful though that you’re using the right bits of the Pythagorean Triple – if 20 hadn’t been the hypotenuse side, we wouldn’t have been able to use that triple, since 20 is the largest of the three numbers in the triple.
Answering using a square root sign
Some questions will ask you to give the length of the unknown triangle side exactly. Say you get down to the point where you’re working out the length of the unknown side ‘x’:
![]()
We could find the square root of 26, but this gives us an endless number of decimal places, and our calculator can only display 9 of them:
![]()
This is not an exact answer, it’s very accurate, but it’s not exact. The only way you can give the answer exactly is to leave the answer in the form before you actually calculated the square root:
![]()
Some questions may want you to answer using this exact form, others may want you to write a decimal number. If the question doesn’t make it clear, you can always do both:
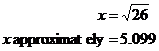
Or using the ‘approximately equals’ symbol:
![]()
Handy Hint #2 - Drawing a line exactly ![]() units long
units long
This may seem impossible to do – try calculating what the square root of 29 is using your calculator. You should get something like this:
5.385164807
Although this answer is very accurate, it’s not exactly right – you could plug this question into a computer and you might be able to get the answer with say 500 decimal places instead of just 9. But the answer would still not be exactly correct, because the square root of 29 is a number with an endless number of decimal places.
So how can you draw a line that is
exactly ![]() units
long? Well, since we’re in a section on Pythagoras’ Theorem, this should tip
you off about how to do it. Notice how the line we want to draw is the square
root of 29 long. For right-angled triangles, when we go to find the length
of the longest side, the hypotenuse, we usually square the lengths of the other
two sides, and then take the square root of that.
units
long? Well, since we’re in a section on Pythagoras’ Theorem, this should tip
you off about how to do it. Notice how the line we want to draw is the square
root of 29 long. For right-angled triangles, when we go to find the length
of the longest side, the hypotenuse, we usually square the lengths of the other
two sides, and then take the square root of that.
So if we can draw a right-angled
triangle where the squares of the two short sides add up to 29, the hypotenuse
side will be exactly ![]() units long. So we need to
think of two numbers, that when squared, add up to 29:
units long. So we need to
think of two numbers, that when squared, add up to 29:
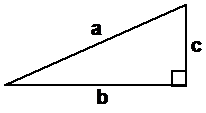
If ![]() , then we’ll know that the length of
side a is exactly
, then we’ll know that the length of
side a is exactly ![]() units long. So what are two
numbers that when squared, add up to 29? This is where you need to try a few
different numbers:
units long. So what are two
numbers that when squared, add up to 29? This is where you need to try a few
different numbers:
What if ‘c’ was ‘1’, then:
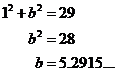
This isn’t much good – now we have an inexact value for the length of ‘b’, which means we can’t draw the ‘b’ line exactly the right length. What about if ‘c’ was ‘2:
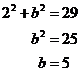
Bingo! If we have c = 2 and b = 5,
then together their squares add up to 29. So this is how we can go about
drawing a line which is exactly ![]() units long.
units long.
Draw two connected lines at right angles to each other, with one line 2 units long and one line 5 units long:
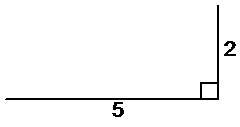
Now, according to the mighty Pythagoras’ Theorem, if we draw a straight line to complete the triangle, the length of that line will equal the square root of the squares of the other two sides:
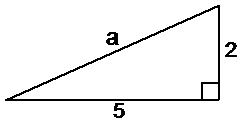
So once we’ve drawn the third side in, the length of ‘a’ can be calculated like this:
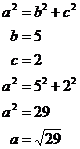
So the hypotenuse of this triangle is
a line exactly ![]() units
long. It’s good to remember this procedure just in case a question comes up in
an exam asking you to draw a length like this exactly. Of course, because
you’re not perfect with your pen or pencil and because you can’t measure
exactly with your ruler, it’s never going to be perfect, plus you probably
won’t be able to draw exactly a 90 degree angle in the triangle. But this is
at least a theoretical way you could draw the line exactly the right
length.
units
long. It’s good to remember this procedure just in case a question comes up in
an exam asking you to draw a length like this exactly. Of course, because
you’re not perfect with your pen or pencil and because you can’t measure
exactly with your ruler, it’s never going to be perfect, plus you probably
won’t be able to draw exactly a 90 degree angle in the triangle. But this is
at least a theoretical way you could draw the line exactly the right
length.
Practical Pythagoras’ Theorem questions
There are lots of types of questions involving Pythagoras’ Theorem and real life situations which you can get on an exam.
|
Jason and Bob are on a reality TV show. They’re the final two contestants, and it’s come down to the final contest. They start at the corner of a large, rectangular, artificial lake. At the far corner of the lake, there is a 1 million dollar prize. Jason is only allowed to swim. Bob is only allowed to jump - to slow him down he’s had his legs tied together. How much faster will Bob have to jump in order to get to the money before Jason does?
|
|
Solution |
|
First things first, we need to work out what path each person is going to take. Jason’s only allowed to swim, so he’s most likely going to take the most direct route to the other corner. Bob has to stay on land, so he’s going to have to go around the boundary of the lake. He can go either way round, they’re both the same length:
So the length of Bob’s total journey is easy to calculate – we just need to add up the two side lengths:
For Jason’s route we need Pythagoras’ Theorem (surprise surprise):
So obviously, Jason’s route is shorter because he
has the most direct path to the money. The question is asking how much
faster than Jason Bob is going to have to cover his distance, to get to the
money first. If Bob had twice as far to travel, then he’d have to travel
just over twice as fast to get there first. In this case, Bob has |