Let’s forget about mathematics for a moment.  If I say something like “I only have a fraction of an apple left” what do I mean?  I mean that I only have part of the entire apple left, probably because I have already eaten some of it.  I could also say something like “I only have half an apple left”. 

So a fraction of something means only a certain part of the entire thing.  Look at the shape below:

What fraction of this shape is dark?  If you look at the shape, you can see it is made up of four squares.  One out of four of these squares is dark.  So I could say something like, “One out of four of these squares is dark.”  But I want to know what fraction of the shape is dark.  So instead, I would say something like, “One quarter of the shape is dark.”  I could also say, “One fourth of the shape is dark.” 

Let’s try another example:

In this picture, what fraction of the shape is dark?  Well, looking at the picture, I can see that the shape is made up of eight squares.  And only one of these squares is dark.  So one out of eight squares is dark.  To answer the question, “One eighth of the shape is dark.”

Writing fractions

So now we know a little about fractions.  How do we write fractions in proper mathematical notation?  Let’s take a simple fraction – “one fourth”.  Well, first let’s change how we say that fraction.  Instead of “one fourth” let’s say, “one out of four.”  Now, to write the fraction, write down the first number you just said:

                                                                  1

Now draw a short horizontal line underneath the number you just wrote:

                                                                

Now write the second number you just said underneath this line:

                                                               

And there you go!  You’ve just written a fraction.

Okay, let’s try a slightly more complicated question.  Write down the fraction of the shape below that is dark:

 

Well, first we look at the shape and work out that 3 out of 8 of the squares are dark.  So, I take the first number and write that:

                                                                  3

Then I add a horizontal line underneath this number:

                                                                

The last thing to do is write down the second number, 8:

                                                                

And I’m finished.  You may want to use the fraction you’ve just written in a complete sentence:

                                                “ of the shape is dark”

Fractions can be written in lots of different ways.  Below are some other ways you can write this same fraction.

One thing that these different ways of writing a fraction have in common is that they involve two numbers.  The general form of a fraction is:

                                                      

So for 3/8, the numerator is 3 and the denominator is 8.  Often the numerator and denominator are described as the “top and bottom” of a fraction.

Proper fractions

Proper fractions are fractions where the numerator is smaller than the denominator.  The following fractions are proper fractions:

                                                  

Equivalent fractions

The same fraction can be written using different numbers.  For instance, let’s try working with a very simple fraction, one half:

                                                               

Now, with proper fractions, you are allowed to multiply or divide the numerators and denominators, as long as you do the same thing to both.  For example, we could multiply both the numerator and the denominator by 10 and we would have an equivalent fraction:

                                                         

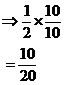
Remember, we can also divide too. For instance we could divide top and bottom by 5:

                                                         

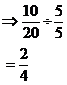
So 2/4 is another fraction that is equivalent to 1/2.

Improper fractions

Improper fractions have denominators that are larger or equal to the numerator.  Improper fractions are numbers that are larger or equal to one.  The following fractions are improper fractions:

                                                     

Mixed numbers

Improper fractions can also be written as mixed numbers.  Say we have the improper fraction 7/5.  We could also describe this fraction as “seven fifths”.  Now, we know that “five fifths” make one.  So let’s split up our fraction like this:

                        

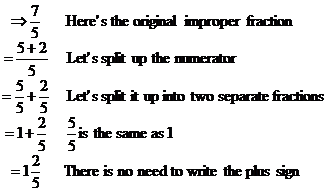
The last term shown above is known as a mixed number, simply because it mixes both whole numbers and fractions.  Mixed numbers can also be converted back into improper fractions.  Say we start with this mixed number:

                    

Reciprocals

The reciprocal of a fraction is like a fraction’s partner.  To find the reciprocal of a fraction, all you have to do is swap the numerator and the denominator.  Let’s find the reciprocal of a simple fraction, 7/9:

                                

Reciprocals have an interesting property.  When you multiply a fraction by its reciprocal you get 1.  We can do this with the fraction we were just working with:

                                                          

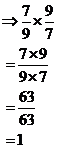
You can also find the reciprocals of whole numbers.  For instance, to find the reciprocal of 5, you have to remember that:

                               

Simplifying fractions

Fractions are not always given in their simplest form.  For instance the fraction  can be simplified all the way down to .  To simplify a fraction, you need to find the greatest common factor (GCF) for the numerator and denominator. 

So say we had a fraction .  To simplify this fraction we first have to find the GCF of 63 and 98:

·         63 has factors 1, 3, 7, 9, 21

·         98 has factors 1, 2, 7

·         The largest common factor is 7.

·         So the GCF of 63 and 98 is 7.

Now what do we do with this GCF?  Well, we use it to divide both the numerator and denominator of the fraction:

                                                         

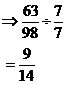
 is the simplest form of .

Greatest common factor

First of all, this is often abbreviated to GCF standing for (G)reatest (C)ommon (F)actor.  The GCF of two numbers is the largest whole number that evenly divides both numbers.  This sounds confusing, so we’ll do an example to show how it all works.

Greatest common factor question

Find the greatest common factor of 24 and 48.

Solution

We need to find the biggest number that evenly divides both 24 and 48.  When you evenly divide something, you aren’t left with a fraction or remainder.  For example, 2 evenly divides 8 since 8 ÷ 2 = 4 exactly, with no remainder.  So let’s see if we can find the GCF of 24 and 48 by starting with 1: ·         1 evenly divides 24 since 24 / 1 = 24 exactly. ·         1 evenly divides 48 since 48 / 1 = 48 exactly. Let’s try a bigger number: ·         2 evenly divides 24 since 24 / 2 = 12 exactly. ·         2 evenly divides 48 since 48 / 2 = 24 exactly. How about 3: ·         3 evenly divides 24 since 24 / 3 = 8 exactly. ·         3 evenly divides 48 since 48 / 3 = 16 exactly. Let’s try 4: ·         4 evenly divides 24 since 24 / 4 = 6 exactly. ·         4 evenly divides 48 since 48 / 4 = 12 exactly. Hmmm…let’s try 5 then: ·         5 does not evenly divide 24 since 24 / 5 = ·         5 also does not evenly divide 48 since 48 / 5 = So what are we supposed to do now?  Someone who has never done this before might be tempted to say that 4 is the GCF of 24 and 48 since it was the last number we tried that divided evenly into 24 and 48.  However, let’s keep going and see where we get, starting with 6: ·         6 evenly divides 24 since 24 / 6 = 4 exactly. ·         6 evenly divides 48 since 48 / 6 = 8 exactly. So, although 5 didn’t divide evenly into the two numbers, we find that 6 does.  So, how do you know when to stop trying larger numbers?  The simple answer is you don’t! To be safe, you need to keep trying numbers until you hit the size of the smallest number – in this case 24. Sometimes the GCF is called the (H)ighest (C)ommon (F)actor – HCF.

Greatest common factor – one technique

Here’s one step by step procedure for finding the greatest common factor.

Greatest common factor question

Find the GCF of 24 and 132

Solution

Step 1: Factors of 24:                 1, 2, 3, 4, 6, 8, 12, 24 Step 2: Factors of 132:               1, 2, 3, 4, 6, 11, 12 Step 3: Common factors:            1, 2, 3, 4, 6, 12 Step 4: The largest number in step 3 is 12 So the GCF of 24 and 132 is 12.

There are also a few different ways you can talk about fractions.  The table below shows ways you can say each fraction:

Fractions as percentages

You can also write fractions as percentages.  For instance, instead of saying “Half of” or ‘’ of you can also say “50% of”.  To work out what percentage a fraction is equivalent to is quite easy.  Let’s try converting 3/8 into a percentage.

First of all, we know that 1 is the same as 100 %.  But in this case, we are not dealing with ones, we are dealing with eighths.  So take that 100%, and divide it by 8.  You may want to use your calculator to do this:

                                                   

Okay, so we have split the 100% up into eight bits, and each bit is 12.5%.  Now, let’s look at the fraction we’re dealing with, 3/8.  Remember that:

                                                          

This is just another way of saying the fraction – we have 3 lots of 1/8^th.  Now, we just calculated that 1/8 is 12.5%.  So if we have 3 of them, then we have:

                                                       

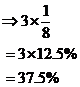
And there we have our answer.  3/8 is the same as 37.5%.