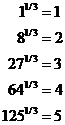There’s a whole heap of laws about how you can do calculations involving indices or exponents. Using these laws you can often make short work of a calculation which would otherwise be very hard to do, even using a calculator.
Adding indices when you multiply
When you multiply together two identical numbers or pronumerals that are both raised to a power, you can combine them together by just adding the indices together:
You’ve got to remember that you can only do this if the bases are identical – in this case they are both ‘x’. Here’s a real number example:
It’s pretty easy to see why this rule works. Writing out this expression the long way by writing every single 4 that needs to be multiplied, you can see how the rule works:
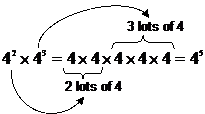
When you have 2 lots of ‘4’ being multiplied by another 3 lots of ‘4’, you end up with 5 lots of ‘4’ being multiplied by each other – which is just the same as 4 raised to the power 5.
Subtracting indices when you divide
When you divide identical numbers or pronumerals each raised to a power, you need to subtract the indices from each other instead of adding them together. For instance, going with our ‘x’ example again:
The index which you need to subtract is always the index above the number or pronumeral which is doing the dividing. In this case, the ‘xb’ term is doing the dividing, so the ‘b’ is subtracted from the ‘a’ index. Here’s a real number example:
It’s easy to see why this works if you write the division in fraction form:
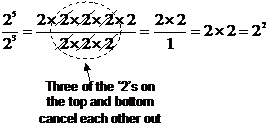
Raising powers to powers
Sometimes you have a normal number or pronumeral raised to some power, we’ll go with our ‘x’ example again:
Then, for some reason or another, you might have to raise this whole term to a power itself:
Here I’ve raised the whole ‘’ term to the power ‘b’. Now, when
you raise a power to another power, you can rewrite the whole
expression, combining the two indices or powers by multiplying them
together:
It’s easy to think about this when you do a real number example, say something like this:
What does the 42 part mean? Well, it means the same as 4 × 4, a multiplication involving two ‘4’s, because of the ‘2’ index. Now, when you raise this whole thing to the power ‘3’, what are you doing? Well, you’re saying, “let’s have three of these whole things multiplying each other.” Let’s write down what this would look like:
So now we can just use the multiplying indices rule, where we add the indices together:
Notice how adding the indices together is just the same as multiplying the original indices by each other:
The zero index or exponent
We’ve come across this before – when you raise anything to the power zero, you end up with the number 1:
One easy way of understanding this I’ve found is to work backwards from higher powers to this zero power, say with something like the number ‘2’:
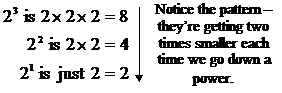
By this pattern, what would 
be? Well, from ‘8’ (23)
to ‘4’ (22), we’ve divided by ‘2’. Going from ‘4’ (22)
to ‘2’ (21), we’ve divided by 2 again. So it makes sense that when
we’re going from 21 (2) to 20, we will need to divide by
‘2’ again. What’s 2 divided by 2? Well, it’s just ‘1’:
Try doing this for any number or pronumeral. You’ll always end up with an answer of ‘1’ when you raise it to the power ‘0’.
Negative indices or exponents
Now, when you raise a number to a negative power, it’s equivalent to the inverse of that number raised to the positive of that power:
We can show why this works by continuing the pattern we used with raising things to the power 0:
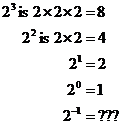
Well, the pattern’s pretty easy to spot – as we go down an index value each time, the answer gets divided by two. So going from 20 to 2-1, we should expect the answer to go from ‘1’ to ‘1 divided by 2’:
This fits with the rule, which is you invert the number and then change the sign of the index:
Note that you can also go the reverse direction with this. Say you have a number raised to a positive index, you can invert it and change it to a negative index:
Evaluating versus simplifying
This is a good time to talk about what the difference between evaluating and simplifying is. Say we’ve got an expression like this:
Usually the question will ask you to simplify something like this. Simplifying gets it in the nicest form, but doesn’t usually come up with an actual numerical answer. You can’t get a numerical answer out of this because we don’t know what the value of ‘a’ or ‘b’ is, they’re just algebraic pronumerals.
However, the question could ask something like this – simplify the fraction, and then evaluate it given that a = 3 and b = 2. Now, to evaluate something usually means to come up with an actual number answer. Because we now know the number value that ‘a’ and ‘b’ represent, we can calculate what the simplified expression is equal to. So the whole process would be something like:
First simplify:
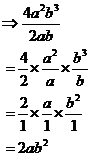
Now for the evaluate step, where you calculate the actual numerical value of this expression:
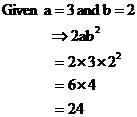
When you’re working with numbers that are raised to powers, it’s usually easiest to simplify the expression as much as possible first, before you evaluate it. For instance, take this expression:
Now, if you just evaluated each of the numbers raised to a power straightaway, you’d end up with some pretty large numbers. Fourteen to the power seven is 105,413,504 for instance. A much better way to evaluate this expression is to simplify it as much as possible first, and then evaluate what you’re left with.
First up, we can simplify the expression in the brackets, because we know that dividing identical numbers raised to powers is the same as just subtracting the indices:
This means that:
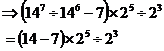
Next up we can simplify the ‘2’s outside the brackets which are raised to different powers:
This means that:
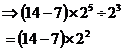
Now that we’ve done all the simplification of the power terms that we can do, we can evaluate what’s left, and calculate the answer:
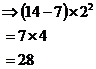
See how much easier the final calculation was after we had simplified everything as much as possible? Doing it this way in an exam saves you time and also makes you less likely to make a mistake, because you do not have to write huge numbers with lots of digits down on the page.
Indices and exponents that are fractions
So we’ve looked at exponents that are positive numbers, and also exponents that are negative numbers? So what about exponents that are fractions? Well, what about something like 21/2? Let’s use our pattern to try and work out what this is equal to:
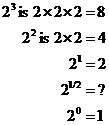
So 21/2 is between 21 and 20.
Well, 21/2 is exactly halfway between 21 and 20.
So there are two equal division steps to get from 21 to 21/2
to 20. The only number that you can divide 2 by twice to get
1 is 
:
Notice how the intermediate value (the value you get after
the first line of calculation) you get is . This is what 21/2 is
equal to – :
In general, anything raised to a fractional power is the same as taking a root of it. Whether that’s a square root, or a cube root, or some other root, depends on the denominator of the fraction. In this previous example, the denominator of the fraction was a ‘2’, so it was equivalent to the square root of the number.
If you have a number raised to the power one third, it’s equivalent to the cube root:
The general way to convert from a fractional power to a root is like this:
Take 51/2 as an example. Look at the fraction, and think about how many halves make up a whole – two. The root you’re looking for is one that if you had two of them multiplying each other, would make up the number 5:
But of course we’re only interested in one of these, so our answer is just:
What about if we had 51/4? Well, the fraction is one quarter. Think about how many quarters make up a whole – four. So the root we’re looking for is one that if you had four of them multiplying each other, you’d get the number 5. The only root which matches this description is the fourth root of 5:
But we’re only interested in one of these roots, so our answer is just:
Fractional indices with numerators larger than one
The next tricky part with fractional indices is when the numerator (top) of the fraction is larger than one, something like this for instance:
The easiest way to deal with something like this is to remember that you can split it up into two lots of ‘2’ multiplying each other, with each one raised to a fractional power with a 1 as the numerator:
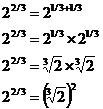
All the normal index laws work with fractional indices just as they do with whole number indices.
Common cube roots
It will help you if you learn a few of the common perfect cube roots – numbers which have a whole number cube root:
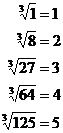
Remember that these could also be written using fractional exponents:
