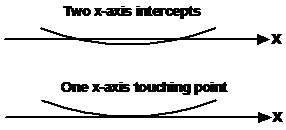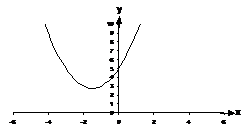You can use a graph of a quadratic function to solve it.  Because you’re reading values off the graph, your answers aren’t going to be exact, but if you draw a decent graph, they should be reasonable.  We’ll solve the following quadratic equation by plotting a parabola on a graph:

                                                      

Now, what we can do is write a function¸ where we replace the ‘0’ in this equation with a ‘y’:

                                                      

We can plot a graph of this function or relationship between y and x, using a set of axes.  The general form of a quadratic function is:

                                                    

For our function then:

                                                            

Since ‘a’ is positive, we know that the parabola will look like a valley.

The turning point coordinates are:

                                                   

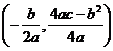
Substituting our values of a, b, and c into this, we get:

                                            

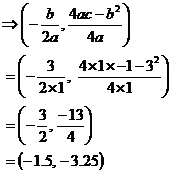
We can find where the graph crosses the y-axis by setting x to 0 in the equation and finding what y is:

                                                  

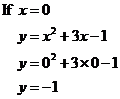
This is enough information to plot the graph.  First of all, we need to draw a set of axes, with the turning point and the y-axis intercept marked on the graph:

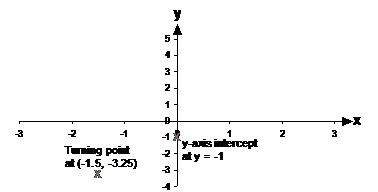
Now, the other piece of information we have is that the parabola is going to look like a valley, so it will start on the left, slope downwards towards the turning point then start sloping upwards as it travels to the right.  We also know that as it travels to the right it’s going to have to pass through the y-axis intercept we have marked on the graph.  Also remember that the slope of the graph gets steeper the further you are from the turning point.  So here’s what the parabola should look like, taking all these things into consideration:

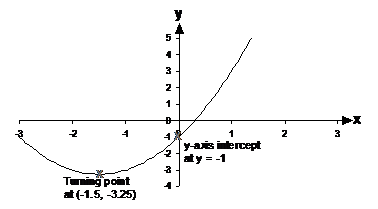
Now, we’re trying to find the values of ‘x’ that make the expression,  true.  Now, when we plotted the graph, we replaced the ‘0’ in the original equation with ‘y’.  So, on our graph, we’re looking for the places where the value of ‘y’ is equal to ‘0’. The places where y is equal to ‘0’ on our graph correspond to where the line crosses over the x-axis.  In other words, we’re looking for the x-axis intercepts.

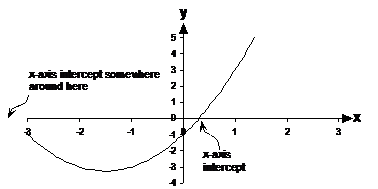
There’s one x-axis intercept just to the right of the origin.  There’s probably also another x-axis intercept a little to the left of x = –3.  What we’re going to have to do is extend the graph a little way in that direction, so that we get the line actually crossing over the x-axis.  To help you do this, it is often useful to calculate a point using your equation.  A plotted point somewhere around the  point would help us extend the line in that area.  So let’s substitute  into our quadratic function:

                                                

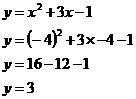
So we know that there is a point on the line at (–4, 3).  We can show this on our graph:

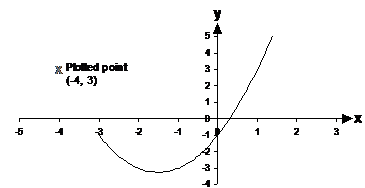
With this plotted point, it is much easier for us to extend the parabolic line to the left on our graph:

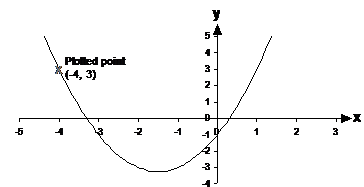
Now we have our two x-axis intercepts.  The values of ‘x’ where the parabolic line crosses through the x-axis are the values of ‘x’ that make the equation  true.  Because we’re reading off a graph and because it’s normally hand drawn, we can’t expect our answers to be too accurate.  For a graph like this, we can probably only expect to get our answers accurate to about one decimal place.

The left x-axis intercept is between –3 and –4.  It look as if it’s just a little less than one third of the way from the –3 towards the –4, so I’m going to say that it’s at x = –3.3.  The right x-axis intercept is between 0 and 1.  It looks to me to be about one third of the way from the 0 towards the 1, so I’m going to say that it’s at x = 0.3.  So my two answers are:

                                         For ,

Notice that I’ve used an ‘approximately equal’ sign to tell the reader that we realise that our answers aren’t super accurate since we’re reading off a graph.

The axis of symmetry

The axis of symmetry is the vertical line that passes through the turning point on a parabola.  Because it’s a vertical line, we only need an x coordinate to describe where the axis of symmetry is.  For instance, the axis of symmetry for the following parabola is just the x location of the vertical line through the turning point:

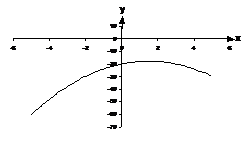
Parabolas of quadratic equations with no solution

Say you’d been asked to find the solution to a quadratic equation by plotting the quadratic function.  What do you do when you get graphs like these ones:

Now normally we look for where the parabola crosses the x-axis.  However, in these two cases, the parabola never crosses the x-axis!  What this means is that there is no value of ‘x’ that will make the quadratic equation associated with the graph true.  For instance, the quadratic function for the left graph is .  The quadratic equation associated with it is exactly the same except with a ‘0’ instead of the ‘y’: .  So what the graph tells us is that there are no values of ‘x’ that will make the equation  true.

Same for the right graph – the quadratic function is .  The quadratic equation is just  or  (the usual way people write the equation is with the ‘0’ on the right hand side).  The parabola not crossing the x-axis anywhere tells us that there are no values of ‘x’ that will make this equation true either.

Parabolas of quadratic equations with one unique solution

Have a look at this graph of a quadratic function:

                                                     

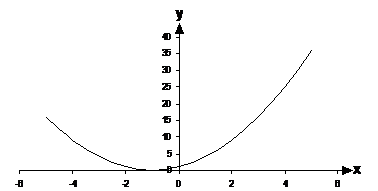
Notice how the parabola in this graph only just touches the x-axis at one point, but never actually crosses over it.  This means that the quadratic equation associated with this graph has only one unique value of ‘x’ that makes it true.  That value of ‘x’ is the value of ‘x’ where the parabola touches the x-axis.  From looking at the graph, it looks like it’s around .  I’ve shown a zoomed in section of the graph to show the touching point a bit more clearly:

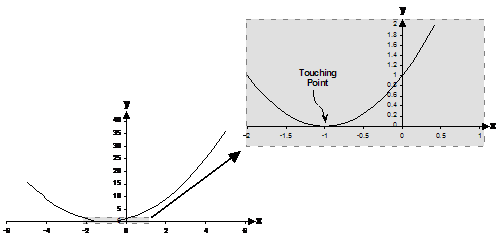
Because of the thickness of your pen when you’re drawing graphs, it sometimes looks like the parabola actually runs along the x-axis for a little while.  In cases like this, it might be best if you replot a zoomed in section of the graph.  This will help you decide whether the parabola is indeed just touching the x-axis in one spot, or whether it does actually cross over and then back again.