Everyone should know their multiplication tables up to 10 by 10.  So for instance, if someone asks you for 7 by 9 you should immediately be able to answer 63.  If someone asks you for 5 by 8 you should immediately be able to answer 40.  If you can learn these basic multiplication tables off by heart then you’ll be able to do many other more complicated mathematical operations without breaking a sweat.

So, say you need to calculate something more complicated, like 43 by 86, and you don’t have a calculator.  Well, there’s nothing for it but to do it the ‘hard’ way, by hand.  First you need to write the two numbers like this:

The first thing to remember when you’re doing multiplication by hand is that you do things from right to left.  This is the opposite direction to how you read, which is from left to right.  A complicated multiplication like 43 × 86 can be done by doing lots of simple multiplications.  The order that you do these simple multiplications is shown in this diagram:

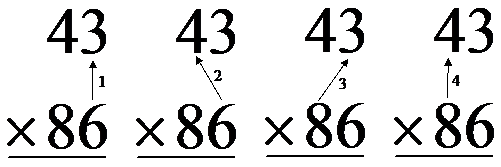
So the first simple multiplication we do is .  If you know your multiplication tables then you should get that .  Now all you have to do is work out where to put this ‘18’.  Whenever you get an answer from one of these simple multiplications, you put the rightmost digit (the ‘8’ in this case) down on the paper, like this:

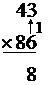
Now what about the ‘1’?  Well, if there are digits to the left of the digit you’re currently using in the top number, this ‘1’ is carried over to be used in your next simple multiplication.  The digit we’re currently using in the top number is the ‘3’, and it does have a digit on its left – the ‘4’.  A good way of remembering that you need to use the ‘1’ in your next calculation is to write it above the digit in the top number that you’ll be multiplying next – in this case the ‘4’:

2

1

The next simple multiplication we need to do is 6 × 4.  From your multiplication tables you should know that the answer to this is 24.  Now this is where we need to remember the amount we carried over from the last simple multiplication – ‘1’.  We add this amount to the 24 and get: 24 + 1 = 25.  We don’t have to do any more carrying because the digit in the top number we’re multiplying doesn’t have any digits on its left.  This ‘25’ we write down next to the ‘8’.  We can also cross out the carried over ‘1’ to remind ourselves that we’ve used it now:

1

2

Now if you look at the four simple multiplications we have to do, shown in the diagram earlier, you’ll notice that we’ve finished all calculations involving the ‘6’ in the ‘86’.  Every time you finish with a digit in the bottom number, you need to do two important things:

·         Start a new line in your calculations.

·         Look at the digit you’re just about to start using in the bottom number – in this case the ‘8’.  Count how many spots it is to the left of the digit in the units place.  Write down that many zeroes on your new line.  The units place is the digit which is used to count ones.

So following these steps, we are about to do the 3^rd simple multiplication.  First we start a new line in our calculations:

1

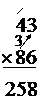
Step 2 is to look at the digit in the bottom number that we’re just about to start using – we’ve finished with the ‘6’ and we’re just about to start using the ‘8’.  We need to count how many spots this ‘8’ is to the left of the digit in the units place. The digit in the units place is the ‘6’.  The ‘8’ is one spot to the left of the ‘6’.  So we need to put down 1 zero on the new line:

 

1

Now that we have done the two steps, we can continue doing our simple multiplications.  The 3^rd simple multiplication is 8 × 3, which from our multiplication tables we know is 24.  Once again, we only write down the rightmost digit – the ‘4’, and we carry over the 2:

This shows that it’s important to cross off carried numbers once you’ve used them – otherwise it would be confusing with all the little numbers written at the top of the calculation.  Now we can do the 4^th and last simple multiplication, which is 8 × 4, which we know is 32 from our multiplication tables.  We need to add the carried over ‘2’ to this number: 32 + 2 = 34.  We write this 34 down next to the ‘40’ we’ve already written.  Don’t forget to cross out the ‘2’ after you’ve used it:

Now we’ve finished all the simple multiplications.  We draw another horizontal line at the bottom of our calculations:

Then we add up the numbers between the two horizontal lines:

And there’s your answer – 43 multiplied by 86 is 3698.

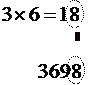
Division by hand – short division

Short division is an easy way of doing complicated divisions by hand.  The best way of showing how to do it is to do an example:

                                                           

In case you haven’t come across these symbols before – this is the same as:

                                                          

In short division the trick is to work your way from left to right, as if you were reading normally (this is the opposite of what you do in multiplication).  So in this case, we start at the left hand side of 2364, so at the ‘2’.  We take this 2, and we try to divide it by 7.  We can’t divide 2 by 7 easily, so we can’t do anything with 2 ÷ 7.  We need to move to the right one digit, but still include the first digit in our calculations.

If we move to the right one digit, we are now looking at ‘23’, instead of just ‘2’.  Once again, we try and divide 23 by 7.  We can divide 23 by 7 – we get a number and a remainder.  How many times does 7 divide into 23?

Well, 7 × 1 = 7, which is smaller than 23.  7 × 2 = 14 which is smaller than 23.  7 × 3 = 21, which is still smaller than 23.  7 × 4 = 28, which is larger than 23, so we’ve gone too far.  Let’s go back to 7 × 3 = 21 – you can fit 3 lots of 7 and then a bit more on top of that into 23.  The remainder is what’s left of 23 when you subtract 3 lots of 7:

                                                          

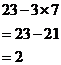
So 23 ÷ 7 gives you 3 and a remainder of 2.  In mathematical notation:

                                                    

We take the ‘3’ and write it on top of the line above the right hand side of the ‘23’.  The remainder of 2 gets carried over and written underneath the line above the next digit to the right:

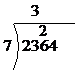
Now that we’ve been able to divide the ‘23’ by 7, we can forget about it now, and move one more digit to the right – to the ‘6’.  Now, the little ‘2’ that we carried over to above the ‘6’ comes into play now – we treat it as if it was in front of the ‘6’ – which gives us ‘26’.  We try and divide this 26 by 7:

·         7 goes once into 26 and leaves a remainder of 19

·         7 goes twice into 26 and leaves a remainder of 12

·         7 goes three times into 26 and leaves a remainder of 5

·         7 doesn’t go four times into 26

So in mathematical notation:

                                                    

We take the ‘3’ and write it above in our answer, and the ‘5’ gets carried over to the right.  Don’t forget to cross out the carried over ‘2’ as we have used it.

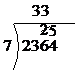
Now we can move on to the next digit to the right – the ‘4’.  It has a ‘5’ above it, so we put the ‘5’ in front of the ‘4’ as if it was ‘54’, and try and divide this by 7.  7 divides 7 times into 54, with a remainder of 5.  We can put this 7 in our answer, and cross out the carried over ‘5’ now that we’ve used it:

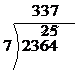
Since we are at the units digit of the number we’re dividing, and we’re still left with a remainder, we know that 7 does not divide evenly into 2364.

Using short division we can calculate answers with decimal places in them.  All we have to do is add a decimal point to the answer and to the number we’re dividing, as well as adding some zeros to the right of the number we’re dividing:

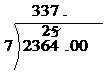
Then we can continue with our division, carrying over the ‘5’ to the first zero:

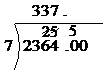
Looking at the first zero, there is a ‘5’ above it, so we treat it as if it was ‘50’.  50 divided by 7 gives 7 with a remainder of 1.  We write the 7 in our answer, to the right of the decimal point, and carry over the 1 to the next zero.  Don’t forget to cross out the carried over ‘5’:

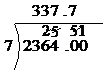
The next digit to the right is a zero, with a little ‘1’ above it carried over – so we treat is as if it was ‘10’.  10 divided by 7 gives 1, with a remainder of 3:

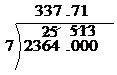
We can do this all day and get as many decimal places as we want.  However, once you’ve got one or two decimal places, you’ve demonstrated to your teacher that you know how to do division by hand.  In an exam the question should specify how many decimal places you have to work out your answer to.  Sometimes your teacher has a general rule that you should give a certain number of decimal places in your answers.

If, as you calculate the decimal part of your answer, you get the same pattern of digits over and over again, your answer is recurring. For instance,  is recurring, it evaluates to . You can put a dot above the repeating digit to show it’s a recurring answer. If the recurring pattern is more than one digit long, you can put a horizontal bar over the repeating pattern. For instance, .