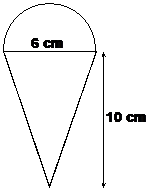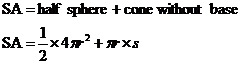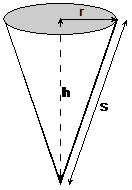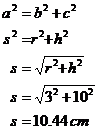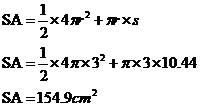Think about an ice cream cone you can buy from a shop – it’s an example of a composite solid shape. The top part of it – the ice cream part – is a sphere, but the bottom part is a cone.
Sponsored Links

Surface area of a cylinder
The surface area of a cylinder is easy to work out because its surface is actually a composite of regular plane shapes. There are two identical circles – one for the top, and one for the bottom of the cylinder. There’s also a rectangle, which is the shape you get when you unwrap the curved surface and lay it flat:
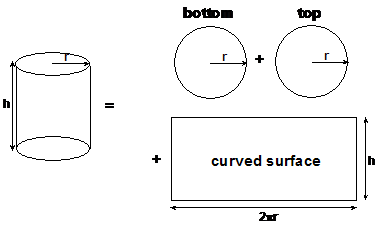
You can convert this into a formula for the surface area by using the formulas for finding each plane shape’s surface area:
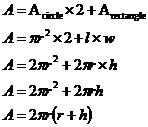
|
Find the surface area of an ice cream cone, where the vertical height of the cone is 10 cm and the diameter of the ice cream sphere is 6 cm. Assume that exactly half of the sphere is exposed (the top half obviously). |
|
Solution |
|
Sometimes the hardest bit in these questions is being able to convert the description of the shape into an actual diagram. In this case, we know we’re trying to draw an ice cream cone, but we’ve got some more detailed information about its dimensions. We also know that only the top half of the sphere is poking out of the top of the cone. So our initial diagram would look something like this:
Now, to work out surface areas of composite solid shapes like this one, you need to work out the surface areas of the bits and then add them together. You have to be careful to watch that the formula that you’re using for the surface area of a regular shape matches what you’ve got. For instance, the general formula for the surface area of a cone is: However, a normal cone has both the curved part and a circular base. The ice cream cone we’ve got doesn’t have a circular base – that’s where the sphere goes. So we want a cone area formula for just the curved surface of the cone. We can multiply out the brackets to see which part corresponds to which surface: So the surface area of just the curved surface of the
cone is The overall area of the composite shape is going to be: There’s only one problem with this – we have the vertical height of the cone, not the slant height. However, we can work out the slant height by using Pythagoras’ Theorem:
Now we can work out the total area of the ice cream cone: |
Here are some common ‘bits’ of shapes that you will encounter in these composite area problems:

Work out the surface area of a normal cylinder with the same radius and height, but multiply by the appropriate fraction. For instance, one quarter for the fractional cylinder shown in the diagram. Then add the areas of the two rectangles that have been revealed by cutting the cylinder up.
![]()
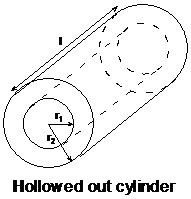
Hollowed out cylinders have these following bits of surface area you need to work out:
· The area of the curved surface inside the hollowed out section – this is a rectangle
· Area of the two disks at each end
· Area of the outer curved surface – another rectangle
The formula for the total surface area of this shape is:
![]()