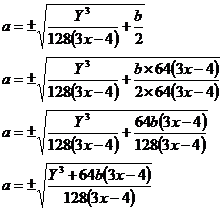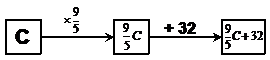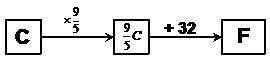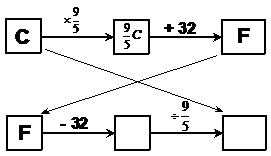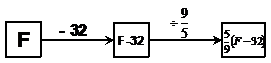Often you are given an equation where it’s not in the form you want it. For instance, say I knew the volume of a sphere, and I wanted to find out its radius. The normal arrangement of the formula for the volume of a sphere is this one:
Sponsored Links
![]()
Of course, if we’re trying to work out the radius, we want this equation in the form “r = something…” To transfer this equation into this form, we can use a box story. First, we write the box story for the current equation. In the first box, we want to put the variable which we want by itself in the equation – in this case this is the ‘r’:
![]()
Now, the result in the final brackets is just the final equation for the volume of a sphere, so we can just write ‘V’ for volume in it instead:
![]()
The box story shows what we need to start with and what operations need to be performed in order to get the volume V. We want to know what needs to happen to just get ‘r’. We can do this by emptying all the boxes, except for the rightmost one, and working backwards through the box story, from right to left. Remember that when we go from right to left, we use the opposite operation. So instead of adding, we subtract. Instead of multiplying, we divide. Instead of squaring or cubing, we take the square root or cube root.
This diagram shows the first box story, and also the new box story, which is in the opposite order, with the opposite operations, and all empty boxes except for the V. Notice how the ‘r’ box in the first box story corresponds to the final box in the new box story. If we work through this new box story, when we get to the final box we will have something that is equivalent to ‘r’.
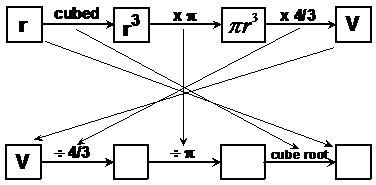
The first step consists of going from the ‘V’ box, and dividing by four thirds instead of multiplying. I’m going to write this new box story from left to right:
![]()
The next step involves dividing by pi:
![]()
The last step involves taking the cube root of this. The result we get in the final box is equivalent to ‘r’:
![]()
So by working through the box story in reverse, we have obtained an expression for what ‘r’ equals – the result in the final box of our new reversed box story:
![]()
|
Bing is making a complicated chocolate cake. He’s found an American recipe for cake on the Internet, the only problem is that all the temperatures are in Fahrenheit, and he’s in Australia, and only has a thermometer that measures Celsius. One part of the recipe says to heat a mixture slowly until it reaches 122 degrees Fahrenheit before adding in the cream. Use a box story to find out what temperature in degrees Celsius Bing should heat the mix to before he adds in the cream. The standard formula for getting Fahrenheit from Celsius is: |
|
Solution |
|
We’ve got a temperature in degrees Fahrenheit, and we want to know what it is in degrees Celsius. Our formula in its current form only gives us degrees Fahrenheit from degrees Celsius, so it’s not much use. We need to rearrange it so that it is in the form, “C = something…,” so we can use it to convert our Fahrenheit temperature. To do this, we need to write a box story, with ‘C’ as the first box, showing how we get to F:
The last box is the Fahrenheit formula, so we can replace it just with ‘F’:
Now, we want ‘C’ by itself, as in “C = something…” We can get this by reversing the box story, clearing all the boxes except the ‘F’ and working backwards. The result we get in the final box of the new box story will be equivalent to ‘C’:
If we work through the new box story, we get this:
The final box in this new box story is what ‘C’ is equal to, so we can write our new rearranged equation: Now we can calculate Bing’s desired temperature: |
Complicated equation rearrangement
Sometimes you need to rearrange a very complicated equation into a different form. The variable you want to rearrange the equation in terms of can sometimes seem to be buried very deep in the equation, so that there’s no possible way you could ever get it by itself on one side of the equation. To avoid getting confused, just try and approach it in a simple, step by step manner, like for this following equation:
![]()
Say we had to rearrange this equation in terms of ‘a’. This means that we want the equation in the form, ‘a = something…,” with ‘a’ by itself on one side of the equation. First we need to look at all the terms that have ‘a’s in them. For this equation, it’s just the term on the right hand side – a very complicated term. ‘a’ is somewhere deep inside it.
To start the ball rolling, what we want to do is gradually chip away at the stuff surrounding the ‘a’, starting from the outermost layer. In this case, the 4 multiplying the square brackets is the outermost layer. We can get rid of this 4 by dividing both sides of the equation by 4:
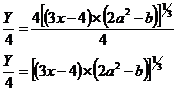
Let’s keep chipping away. Now, the outermost layer of the term with the ‘a’ in it is the ‘raised to the power one third’ bit. We can get rid of this by cubing both sides of the equation:
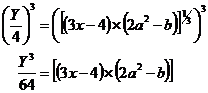
It’s starting to look a little bit better. Now the outermost layer stopping us from getting directly at the ‘a’ is the first set of brackets – the ‘3x – 4’ bracket which is multiplying the brackets containing the ‘a’. We can get rid of these by dividing both sides by ‘3x – 4’:
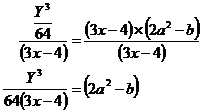
We’re getting close! The next outermost layer stopping us is just the ‘–b’ bit. We can get rid of this by adding ‘b’ to both sides:
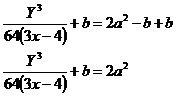
Next step, get rid of the ‘2’ in front of the ‘a2’ term:
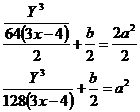
Last step – get rid of the power ‘2’ above the ‘a’, by square rooting both sides:
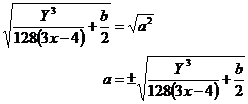
Usually you change the order so the variable you’re interested in (the ‘a’) is on the left hand side of the equation. You can also neaten up the fraction under the square root by combining it into one fraction, by changing each fraction so they have the same denominator and then adding them together: