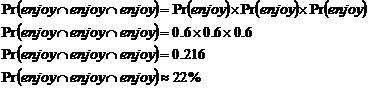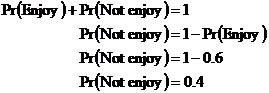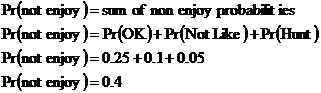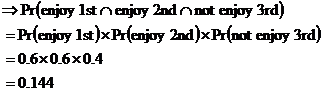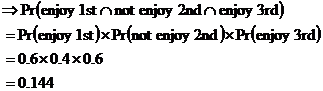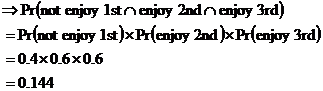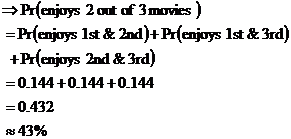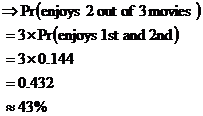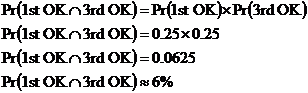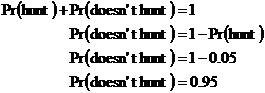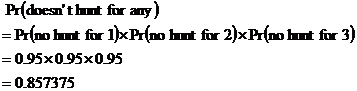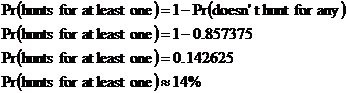Two events are mutually exclusive if they can’t happen at the same time. For instance take flipping a coin – heads and tails are mutually exclusive events since you can only get one or the other.
When events are mutually exclusive, there is no overlap of their probabilities. This means that if you want to work out the probability of either event A or event B happening, and they are mutually exclusive, then you can just add their individual probabilities:
Sponsored Links
![]()
Remember that the ‘U’ symbol is the union
symbol, which is like ‘or’ – so in this case ![]() means the probability of event A or
event B happening.
means the probability of event A or
event B happening.
|
Most people have seen the whole range of movies at the cinema – great ones, OK ones, and really, really bad ones. Sean is not very fussy about his movies and tends to enjoy most of them. When he goes in to see a new movie, there is a 60% chance he enjoys it, a 25% chance that he finds it OK, a 10% chance that he doesn’t like it at all and a 5% chance that he will hunt down the director to impart justice. Calculate, using proper mathematical notation, these probabilities for the next 3 movies Sean sees: (a) Pr (enjoys all the movies) (b) Pr (enjoys only 2 out of the 3) (c) Pr (finds the first and third movie OK) (d) Pr (hunts the director for at least one of the movies) |
|
Solution |
|
(a) Now, does what Sean thinks of the first movie affect what he thinks of the second movie? No! This means what Sean thinks of each movie is a set of independent events. So we can use this rule: Now we know that Using our rule for independent events, we can work out the answer:
(b) This is a bit trickier, asking us what are the chances that he’ll enjoy only two out of the three movies. This means any two of the three movies – so he could enjoy the 1st and the 2nd, or the 1st and the 3rd, or the 2nd and the 3rd movies. This means we’ll have to work out the probabilities for each of these three cases. First up, the case for when he enjoys the 1st and 2nd movies: Now, if he enjoys only the 1st and the 2nd movie, this means he can’t enjoy the third. So we are interested in this probability: Now once again these are independent events – what Sean thinks of the 2nd movie for instance isn’t affected by what he thinks of the 1st or 3rd movie. This means we can get our final answer by multiplying individual probabilities together: Notice that in this case he doesn’t enjoy the
3rd movie, which is why we have the We know that the probability of enjoying any one movie is 0.6. Enjoying a movie is mutually exclusive to not enjoying a movie – you can do one or the other. When two events are mutually exclusive, this means that their probabilities add to give 1: The other longer way of calculating this would be to add up all the other probabilities: Either way you get the same probability – there is a 0.4 chance that Sean will not enjoy any one movie he sees. We can use this information in our original equation to work out the answer: Just need to work out the probabilities for our other two cases where Sean enjoys two out of the three movies. There’s the case where he enjoys the 1st and 3rd movies: And the case where he enjoys the 2nd and the 3rd movies: So the total probability of Sean enjoying two out of the three movies is the sum of the probabilities of each of these three cases: We could have saved ourselves quite a bit of time by realising that all three cases were identical as far as probabilities go – the chances of Sean liking the 1st and 2nd film are the same as for him liking the 1st and 3rd film. So we could have just worked out the probability for one case, and multiplied it by 3:
(c) This one’s relatively easy, we can write a mathematical expression straightaway for what we want to find: What about the 2nd movie – well, it can be anything. This question doesn’t specify anything about how he finds the 2nd movie, just about how he finds the 1st and 3rd movie OK. This means the 2nd movie can be anything – enjoyed, OK, not liked, or bad enough to cause a director hunt. So we only need to worry about the 1st and 3rd movies in our calculation. How Sean finds them are independent events that don’t affect each other, so we can use the multiplication of individual probabilities rule: (d) We have to find Pr (hunts the director for at least one of the movies) This is an ‘at least’ question. It’s often easier to solve these questions by considering the mutually exclusive case. For this question, the mutually exclusive case is: Probabilities of mutually exclusive events add to 1: We can rearrange this: All we need to do is find The probability for one movie that Sean hunts down the director is 0.05. The probability for one movie that Sean doesn’t hunt down the director is a mutually exclusive event, so their probabilities should add to 1: We can use this in our previous equation: Now we can go back to our original equation: This is a good thing for the directors of the three films – there is a pretty low probability any of them will get hunted by Sean for producing a really, really bad film. |
Expected number for a certain outcome
Sometimes you’re asked to estimate how many times you would expect to get a particular outcome, if you performed an experiment quite a few times. A very simple example would be:
How many times would you expect to get ‘heads’ if you flipped a coin 100 times?
To work this out, you need to know the probability of the outcome happening for one experiment or trial, and then multiply this by the number of trials.
The probability of getting a ‘head’ from one coin flip is 50%, or 0.5. What you do is take this ‘0.5’, and multiply it by the number of trials – 100 in this case:
![]()
There’s your answer – you’d expect to get 50 ‘heads’ if you flipped a coin 100 times. Now of course, if you went out and flipped a coin 100 times, you wouldn’t necessarily get 50 heads. You might get 43, or 54. This is because probabilities are not certainties. So even though we’d expect 50 heads, we could get more or less.
But in general, to estimate how many times you’d expect an event to happen, do this:
![]()
Average run length of an outcome
Say you went and flipped a coin 10 times, and recorded what you got, in order:
H, T, H, H, T, H, T, T, H, H
If you look at the sequence you recorded, you can see that there are ‘runs’ of heads – sections in the sequence where only heads occur. I’ve shown these runs here:

So reading from left to right, there’s a run of 1 head, then a run of 2 heads in a row, then another of 1, and finally a run of 2 heads in a row. You can find the average run length by adding up these run lengths and dividing by how many different runs there are:

Average run lengths for large numbers of trials
When you do a certain trial or experiment lots and lots of times, there is a formula you can use to calculate the average run length of a particular event:
![]()
You take 1, and divide it by 1 minus the probability of the event happening in one trial. In the case of flipping a coin, the probability of getting a ‘head’ in one trial is 0.5. So the average run length of heads if you flip a coin a lot of times is:
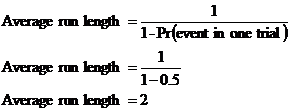
This surprises some people who expect that you would get a shorter average run length from flipping a coin.
This formula only works when the trial or experiment is repeated lots of times (I use 100 as being ‘lots’), and when the outcome of each trial is independent of any other trials.