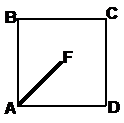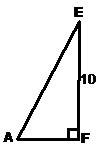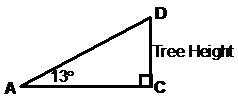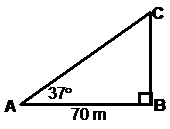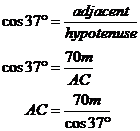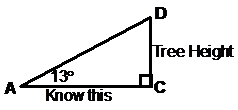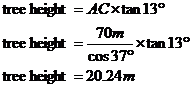Three-dimensional trigonometry problems
Three-dimensional trigonometry problems can be very hard and complex, mainly because it’s sometimes hard to visualise what the question is asking. If there is a diagram given in the question it can make things easier, but it can still be challenging thinking about exactly what you need to do to find an answer. It pays to keep a calm head and think about exactly what you need to find and all the things that you know.
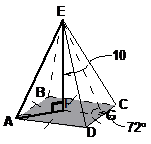
Usually these 3D questions will require more than one step to solve. For instance, take this classic pyramid type question, where you need to find the length AE:
Sponsored Links
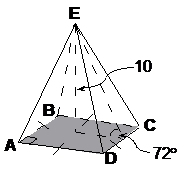
3D diagrams are usually more complex than 2D ones and have more information present in the diagram. This one shows a pyramid. The four dashes through the four sides of the base show that all four sides are equal in length, and the right angle shown in one corner of the base tells us for certain that the base is a square (if all four sides were equal length but there were no angles marked it could be a parallelogram base).
The vertical height of the pyramid (not the slant height) is 10 units. Also we know that the angle formed between the slant line up the middle of a side and the base is 72°.
Here’s where we ask ourselves – what are we trying to find? In this case, it’s given straight to us in the question – the length of side AE. How can we find out this length? Well, there are a couple of triangles which it forms part of, shown here:
Both these triangles are right angled triangles, meaning if we could find the length of both other sides, we could find the length of side AE using Pythagoras’ Theorem. The second triangle option looks attractive, because one of the sides is the vertical part of the triangle, which we already know is 10 units long. So let’s work with this triangle. We just need to find the length of its short side now.
The short side of the triangle forms half of the diagonal of the square base. At this stage it pays to add some more letters into our diagram so we can more easily describe what we’re doing in any calculations. We can also draw a square representing the base, and a triangle representing the one we’re working with in the diagram:
|
|
|
|
So to recap – we know that EF is 10 units long. If we can work out the length of AF, then we can use Pythagoras’ Theorem to work out the length of AE. So how do we find out AF? Well, look at the square base diagram. If we can work out the side length of the square base, we can use Pythagoras’ Theorem to work out the length of AF. So let’s work on the side length of the base.
The only unused piece of information in the question is the 72° angle. Let’s have a look at that triangle:
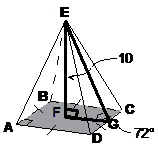
Its short side forms part of the square base. In fact, its short side is exactly half the length of the base’s sides. We can use trigonometry to work out the length of FG, which is half the side length of the base. Here’s the triangle we’re working with:
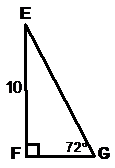
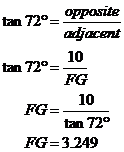
If we go back to our diagram of the base, we now know the length of FG:
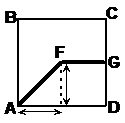
The two lengths marked with arrows are the same length as FG, so we can use Pythagoras’ Theorem to work out the length AF:
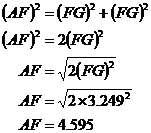
We can go back to our original triangle with the side AE in it that we’re trying to find. We now know the lengths of the other two sides (AF and EF), so it’s just Pythagoras’ Theorem to find AE:
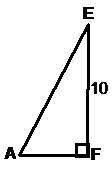
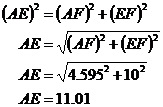
Notice how many 2-dimensional diagrams I drew along the way. It makes it easier when you start off with the 3-dimensional diagram, and then work at bits of it, by drawing 2-dimensional parts of it and working on each part individually. By labelling the corners and important parts of the 3-dimensional diagram, you can also label the points in these simpler 2-dimensional diagrams. Having labels in both diagrams will help you keep track of where the simple 2D diagrams fit into the 3D one.
|
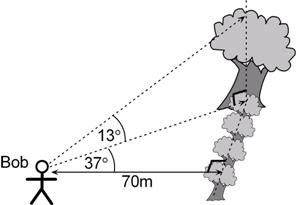
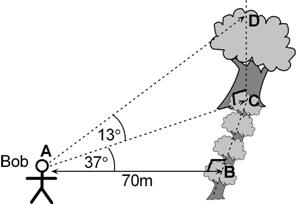
Find the height of the large tree. Bob knows that the angle between the closest point to him in a row of trees and the large tree is 37 degrees. He also knows that the angle of elevation from the ground to the top of the tall tree is 13 degrees.
|
|
Solution |
|
This is a pretty common type of question – there’s an animal or something in the top of a tree like in the diagram: Sometimes the hardest bit of these types of questions is working out which angles are in which plane. For instance, in the diagram, the 13 degree angle is an angle of elevation between the bottom and top of the large tree. The 37 degree angle is a bit more ambiguous. What hopefully the question has is a statement something like this: Bob knows that the angle between the closest point to him in a row of trees and the large tree is 37 degrees. This clarifies that the 37 degree angle is in the ground plane. The right angle at the end of the 70 m line also shows that that point in the trees is the closest point that the question is talking about. Usually the question is asking you to find a length or angle somewhere in the diagram. In this case, the question is asking you to find the height of the large tree. Now we’ve got a right angled triangle with one side that is the height of the tree, and we also know another angle – 13°. All we need is one more side length in that triangle, and we can work out our answer. Let’s label our 3D diagram before we go any further:
The triangle we’re talking about is triangle ACD:
Side CD is the height of the large tree. All we need is the length of another side, either AD or AC. Let’s work on side AC, since it’s in the ground plane, unlike AD. Now side AC is also part of another triangle, the triangle in the ground plane with the 37° angle and 70 metre side:
For this triangle we have a known side length and we have a known angle. This means we can find out any other side length or angle in it. What we want is the length of side AC. We can use cosine to find this out: Now here’s a trick. Rather than working out the value of AC, let’s just remember this expression for what AC’s length is. Now, back to our other triangle, armed with this new information:
So we now know AC, and we’re trying to find CD. We need to use tangent: This is the part where we substitute in our remembered expression for what the length of AC is: |
