When one variable is proportional to some constant times the other variable, this is known as direct linear variation.  Why linear?  Because the highest power of the variable being multiplied by the proportionality constant is 1.  This means that graphs of a direct linear relationship have these characteristics:

·         The line is a straight one

·         This straight line always passes through the origin of the graph (the 0, 0 point where the axes usually intersect)

From a graph

One type of question will give you graphs and ask you to identify whether there is a direct linear relationship:

Direct linear relationship		Not a direct linear relationship

From an equation

In trying to recognise a direct linear variation from an equation, you want to get the equation into a form where there’s one variable on each side of the equals sign.  Then, if both variables are raised to the power ‘1’, and you’ve got no other terms, then you’ve got yourself a linear relationship:

Direct linear relationship	Not a direct linear relationship

Sometimes the equation will need rearranging before you can work out whether it is a direct linear relationship or not:

                                                      

This one was, but this next one isn’t:

                                                         

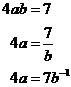
Although ‘a’ is raised to the power ‘1’, ‘b’, because it comes from the bottom of a fraction, is actually raised to the power ‘–1’ in the final line.

From a table of data

It’s pretty easy to tell if there is a direct linear relationship in a table of data.  Just assume that there is one, and work out the value of the proportionality constant from that.  Then use the formula to check the other values in the data set.  For instance, if we were given:

So take the first pair of data values, and use them to work out the value of ‘k’:

                                                          

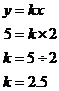
So:

                                                          

Then use this equation to check the other values in the table.  For x = 3:

                                                         

This agrees with the ‘7.5’ in the table.  For x = 4:

                                                         

That’s fine too, only have to check x = 5:

                                                         

This however does not agree with the y value of ‘12’ in the table.  This means the data in the table is not part of a direct linear relationship.  You could however remove the last column of data, and then the remaining data would be part of a direct linear relationship.

Making cordial question

Sally loves her cordial mixed just right.  After she’s poured the cordial concentrate into a glass, she likes to add four times as much water into the glass.  Write down the quantitative rule or relationship telling us how much water she needs to add depending on the amount of cordial.

Solution

What are the two variables in this question?  Well, there’s the amount of cordial concentrate, and the amount of water.  We’ll use ‘C’ and ‘W’ to represent each one.  Now, for every unit of cordial she adds, she likes to add another four units of water.  The size of the unit doesn’t matter – all that matters is the relative amounts of each liquid.  For instance, in a glass she might have 50 mL of cordial, and four times as much water – 200 mL of water.  In a big bottle she might have 200 mL of cordial, and 800 mL of water.  So very simply, there is always four times as much water as there is cordial.  In mathematical terms, we could write this:                                                             In this case, the constant of proportionality is ‘4’, since the general form of a direct linear relationship is:                                                              In this case, the general form is:                                                              If the question had asked us for a rule telling us how much cordial to add given that a certain amount of water had been put in a glass, it would be the other way around.  We’d have an equation like this:                                                            The constant of proportionality in this case would be one quarter – 0.25.