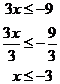Inequations can be solved just like equations, except you need to learn one new important rule:
· If you multiply both sides of an inequation by ‘–1’, you need to swap the direction of the inequality symbol.
Sponsored Links
Swapping the direction of the inequality symbol means you change a “larger than” symbol to a “smaller than symbol” and vice versa.
|
> |
becomes |
< |
|
< |
becomes |
> |
|
≤ |
becomes |
≥ |
|
≥ |
becomes |
≤ |
When you solve inequations, the answer you get
isn’t an exact number. Instead your answer is usually something like, “x is
smaller than 5,” or, “y is larger than or equal to
.”
|
Solve the following inequation for x: |
|
Solution |
|
So in our final answer we basically want x all by itself on one side of the inequation. To get to that stage we’ll need a few steps. At the moment, the x is on the left hand side of the equation. There’s also a 5 on that side – let’s get rid of the 5 by subtracting it from both sides: Now it’s a bit better, but we’ve still got problems. There’s a negative sign in front of the term with the x in it. Let’s deal with the negative sign. You can change the sign of a term by multiplying it by ‘–1’. Let’s do that to both sides of the equation: Uh-oh. What have I forgotten to do? Well, we’ve just multiplied both sides of the equation by ‘–1’ – we need to swap the inequality symbol around. So we need to change it from a “larger than or equal to” symbol to a “smaller than or equal to” symbol: OK, that’s better. Now it’s almost in the right format, we just would like to have the x completely by itself. At the moment it’s got a 3 in front of it. We can get rid of the 3 by dividing both sides by 3: |
Handy Hint #1 - Choosing how to solve questions
It may seem obvious to you, but a lot of students forget to think about what they’ve learnt in the weeks or months before an exam. Chances are that most of the questions in an exam are going to require you to use some of the stuff you’ve recently learnt to solve them.
Say that it’s been six weeks since your last exam, and for those last six weeks all you’ve done is study algebra, algebra and more algebra. You’re now sitting in a new exam and starting to read the first question. It’s pretty likely that to solve a lot of the questions in this exam, you’ll need to use some of that algebra. So remember that when you’re reading the questions.
Sometimes you’ll come across a question which you think you can solve without using stuff you’ve recently learnt. This is fine – often there are many different ways to solve a problem. However, your teacher probably wants you to demonstrate that you can use the material you’ve learnt recently. So, if you can, try and solve the problems using stuff you’ve just learnt. If you can’t do this, then any other way of solving the problem will do just fine.
Using set notation to solve inequations
We’ve already learnt how to solve inequations, such as the following one:
It’s the same process as we use for normal equations, except we have to remember that when we multiply or divide both sides by ‘–1’, we need to swap the direction of the inequality symbol.
Now, there is a more formal mathematical way of writing down an inequality question, using sets. For instance, the last question would be written something like this:
You can read this as “Find the set of x, given that two x plus three is smaller than or equal to seven.” So we could solve this as we normally do:
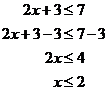
Expressing solutions to inequations on a number line
There is a graphical way of representing the answer to an inequation on the number line. By drawing an arrow along the number line, you can indicate the range of values that the variable can have. For instance, we would draw an arrow starting at 2, pointing in the negative direction:
Notice how I’ve used a small, solid black circle at the
start of the arrow, above the ‘2’ on the number line. This tells the reader that
the solution includes the number ‘2’. If the solution had been 
, then you’d draw
the same arrow, starting at ‘2’, but you’d use a hollow circle to
indicate that the set of x does not actually include ‘2’ itself:
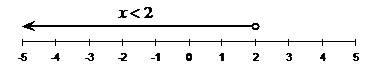
The arrow also tells the reader that the set of x includes all the values in the direction the arrow points – so in this case all the negative values. We can also have a solution where the set of x is a fixed range, like this:
The number line representation for this solution won’t have any arrows in it, but will look like this:
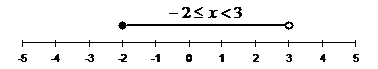
Notice how the line is a finite length – it doesn’t have an arrow on either end pointing for ever in either direction. Instead, we have a solid circle above the ‘–2’ on the number line, telling us that the set of ‘x’ does include ‘–2’. The line runs towards the positive numbers, ending at above ‘3’ on the number line. The circle above ‘3’ is a hollow circle, telling us that the set of ‘x’ does not include ‘3’ itself, but the values leading up to it.
