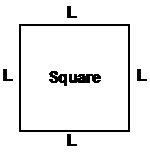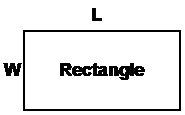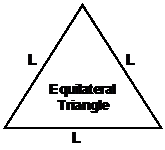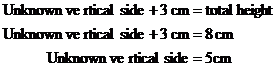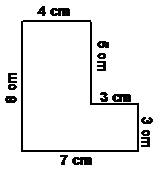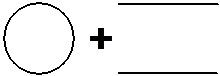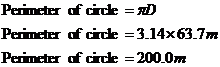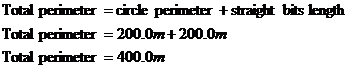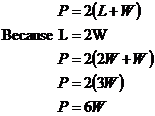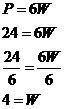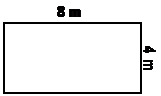The perimeter of a shape is just the distance around its boundary, or edges. Most of the normal shapes have easy formulae that allow you to quickly work out what the perimeter of the shape is. Here are some of the formulas:
|
Sponsored Links |
Perimeter = 4L |
|
|
Perimeter = 2(L + W) |
|
|
Perimeter = 3L |
|
|
Perimeter =
Or
Perimeter = |
A circle is a special type of shape, because it only has one continuous edge all around it, rather then separate sides like in a square. The perimeter of a circle is just over 3 times as long as its diameter. The diameter of a circle is the distance from one side of the circle to the other in a straight line through its centre.
The actual number that you multiply the diameter by to get the circle’s perimeter is called “pi”, which is one of the most important symbols in mathematics. Its value is approximately 3.14159265. Pi is a special number because you can keep writing down digits to the right of the decimal place forever:
=3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196
… and so on and so on…
Now when you’re doing an exam, you’ve got two choices. You can either use a memorised version of pi to do your calculations – most maths teachers are happy if you use “pi to two decimal places” – 3.14 in other words. The other option is to use the pi button on your calculator – when you press the pi button, it’s as if you’d entered pi to about 8 or 10 decimal places yourself.
Length of an arc
A sector is a chunk of a circle like a wedge of cake. Sectors can be very narrow, or very wide. We use the sector angle to describe exactly how big a sector is. The sector in the diagram has a sector angle of about 95°. In the diagram you can also see that the curvy bit of the sector is called the arc length.
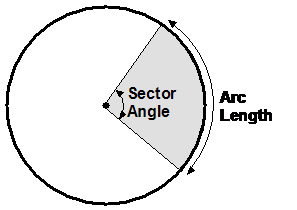
The arc length makes up part of the circumference or perimeter of the circle. But how much of the circumference does it take up – half? Three quarters? Well, it depends on what the sector angle is.
To show what I mean, let’s think about a sector with a sector angle of 360°? What would it look like? Well…it would be just like a circle! How long would its arc length be? Well, it would be the same as the circumference of a circle.
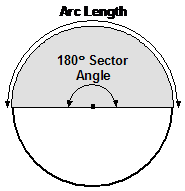
So what about a sector with a sector angle of 180°? How long would its arc length be? Well, 180° is only half of the full 360° required to be a circle, so the arc length would only have half the length of the circle’s circumference:
What about for a 90° sector? Well, 90° is only one quarter of the full 360° required for a circle, so the arc length would only be one quarter of the circumference of the circle. So the fraction that the sector angle is of 360°, is also the fraction that the arc length is of the full circumference. In mathematical terms this would be:
Now we know that the circumference of a circle is
just 
,
so we could rewrite this:
|
A typical question with perimeters will ask you to find the perimeter of a shape you are given in a diagram. However, usually the question won’t have the lengths of all the sides labelled. You have to work out from looking at the diagram how long the unlabelled sides are, and then add all the sides together to get the total perimeter. Here’s an example question: Find the perimeter of this shape:
|
|
Solution |
|
Well, there are six sides in this shape, but only four of them have a length marked on them. Does this mean we can’t do the question – no! All we have to do is work out how long these unlabelled sides are. Let’s deal with the vertical side first. Generally the way to find out the lengths of these unknown sides is to see if we can use other information in the diagram to help us. Notice how on the right hand side of the diagram, there are two vertical bits, our unknown side, and a 3 cm long side. Together, these two vertical sides make up the entire height of the shape. Now if we knew what the total height was we could work out our unknown side. Bingo! If you look on the left hand side of the diagram, there is one long vertical side which is the entire height of the shape – and it’s 8 cm long. This means we know that our unknown vertical side plus the 3 cm vertical side must add up to 8 cm. Do some simple maths and: We can do the same thing to work out how long our unknown horizontal side is. It and the 4 cm horizontal side together make up the entire width of the shape. Do we know how wide our shape is – yes! The bottom side of the shape runs the entire width, and it’s 7 cm long. A little more maths: Now we know the lengths of every side. To find the perimeter, we just need to add them all up. It is also a good idea to label the diagram with the new information we’ve found:
|
|
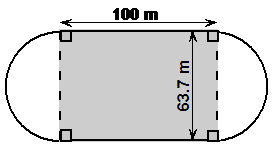
This is another common problem when you’re working with perimeters. It means you have to be able to handle having parts of several different shapes put together in a diagram. Here’s the question: Bob’s building team has just finished a running
track. However, they think they may have made a mistake. One lap of the
running track is supposed to be 400 metres long. Have they done it correctly?
Use
|
|
Solution |
|
The trick with these questions is to realise that the overall shape is made up of simpler shapes and lines. In this diagram, we’ve got two half circles, and also two straight lines. We already know the length of the straight lines – they’re labelled as being 100 metres long. We need to work out the length of the two curvy bits. You can save some time by realising that the two half circles together make up one full circle. So you can work out the whole perimeter by doing a sort of sum of shape perimeters like this:
Which, since the two half circles make a whole circle, is the same as:
The perimeter of the circle we can calculate using
the formula, perimeter = Now we just need to work out the length of the two straight bits. One straight bit is 100 metres long so two straight bits must be…200 metres long! So our overall perimeter is: |
.
|
The other main type of perimeter problem is one where you’re given a perimeter, and you have to work out what the shape looks like. Fencing seems to be a very popular topic for perimeter problems, so we’ll use a fencing problem to show how to work backwards. Here’s the problem: Barry (gotta love these names) has spent $600 on fencing for his rectangular pool. The fencing cost $25 per metre, and he used all $600 worth. His pool is twice as long as it is wide. What are the dimensions (length and width) of his pool? |
|
Solution |
|
So first things first, we don’t actually know how many metres of fencing Barry bought. We can work it out though – he spent $600 total and it was $25 per metre: Okay, so we know that the total perimeter of his
rectangular pool is 24 metres. We have a formula for the perimeter of a
rectangle, So we need to dive back into the question to see if there’s any more useful information. Aha! His pool is twice as long as it is wide, the question says. What does this tell you – that L is twice as big as W. Or in mathematical terms, L = 2W. At the moment we’ve got a formula for the perimeter which has both ‘L’s and ‘W’s in it. How about wherever there is a ‘L’ in the formula we write ‘2W’, since they are the same: Now we have an equation we can use. We know the perimeter is 24 metres, so we can work out what W is: So the pool is 4 metres wide. We know that the length is twice as big as the width. So the pool must be 8 metres long:
If you’ve got a bit of spare time you can quickly check your answer by working backwards. If the pool is 4 metres wide and 8 metres long, then the total perimeter must be 4 m + 4 m + 8 m + 8 m = 24 m. 24 metres at $25 / metre comes out to $600 in total. This is the same amount of money as given in the question, so we’ve probably got the right answer. |
.
This doesn’t help us yet though, because it’s got two unknown variables in it
– L and W. We only know P. 
